可比性究竟意味着什么？

可比性是一个在多个领域中广泛应用的概念，它关乎我们如何理解和分析不同对象之间的差异与相似性。简而言之，可比性指的是两个或多个对象在某一特定标准或尺度下，能够进行有效的比较和衡量。这种比较的基础在于对象间存在某种可作比较的属性或特征，这些属性或特征为我们提供了一个共同的参照点，使得比较成为可能。

在经济学中，可比性常用于不同经济体、行业或企业之间的比较。通过比较不同经济体的gdp、人均收入等经济指标，我们可以了解它们之间的经济发展水平差异。在行业内，企业之间的财务报告可比性则有助于投资者和分析师更准确地评估企业的财务状况和经营绩效。这种可比性分为纵向可比性和横向可比性，纵向可比性关注的是同一企业不同期间财务报告的可比性，而横向可比性则关注同一行业不同企业之间财务报告的可比性。

会计学中的可比性尤为重要，因为它直接关系到财务信息的准确性和可靠性。高质量的财务信息必须具备可比性，以便信息使用者能够准确地了解企业的财务状况和经营成果，从而作出明智的决策。此外，可比性还有助于提高信息披露的透明度和加强监管，降低信息不对称的风险。

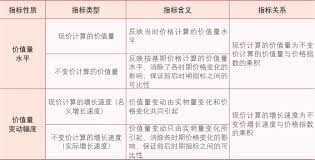
在数据分析和统计学中，可比性是数据分析和比较的基础。为了确保数据的可比性，我们需要确保比较的对象在相同的尺度或标准下进行，同时比较的属性或特征必须是相关的。此外，数据的准确性和可靠性对于可比性至关重要，因此我们需要加强数据收集、处理和分析的准确性和可靠性。

可比性不仅在经济和会计领域有重要作用，在教育领域也同样重要。例如，要比较学生对某门课程知识的掌握程度，我们可以使用考试成绩作为标准。这种可比性使得我们能够客观地评估学生的学习效果，从而制定更有效的教学策略。

值得注意的是，可比性并不是绝对的。在某些情况下，由于对象之间的差异过大或缺乏共同的参照点，比较可能变得困难甚至无意义。因此，在进行比较时，我们需要谨慎地选择比较的对象和属性，以确保比较的有效性和准确性。

此外，可比性还涉及到一些数学和逻辑上的性质。例如，反身性是指在可比性的前提下，对象的任何组合都强于自身；传递性则是指对象之间比较的结果可以传递，即如果a大于b且b大于c，则a必然大于c。这些性质为我们理解和应用可比性提供了重要的数学基础。

综上所述，可比性是一个重要的概念，它有助于我们更准确地了解不同对象之间的差异和相似性。无论是在经济学、会计学、数据分析还是教育领域，可比性都发挥着不可或缺的作用。因此，我们应该重视可比性在各个领域的应用和发展，以推动我们更好地理解和分析世界。

• 上一篇：时尚界新宠：Lisha男装品牌魅力何在？

• 下一篇：CP19发行背后的年份故事