探索奇趣数学：奇函数相乘，结果竟然如此迷人！

在数学的广阔天地中，函数作为一种基本的研究工具，不仅承载着数量关系的变化，还蕴含着众多有趣且深刻的性质。其中，奇函数与偶函数作为函数分类中的重要组成部分，它们各自遵循特定的变换规则，展现出独特的数学美感。本文将聚焦于奇函数的一个重要特性——奇函数乘以奇函数的结果，通过这一简单的数学运算，揭示其背后的深刻含义和应用价值。

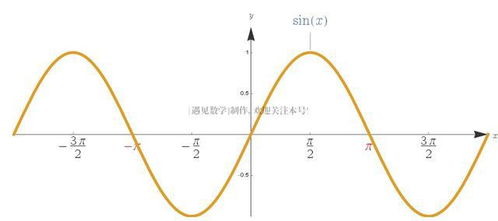
首先，我们需要明确什么是奇函数。如果一个函数f(x)满足f(-x) = -f(x)，那么这个函数就被称为奇函数。直观地说，奇函数图像关于原点对称。例如，正弦函数sin(x)就是一个典型的奇函数例子。而偶函数则定义为满足f(-x) = f(x)的函数，其图像关于y轴对称，余弦函数cos(x)便是偶函数的一个实例。

接下来，我们探讨奇函数乘以奇函数的结果。当我们将两个奇函数相乘时，结果会是一个偶函数。这一结论可以通过简单的代数推导得到证明。假设f(x)和g(x)都是奇函数，则有f(-x) = -f(x)，g(-x) = -g(x)。那么对于乘积函数h(x) = f(x) * g(x)，我们计算h(-x)：

h(-x) = f(-x) * g(-x) = (-f(x)) * (-g(x)) = f(x) * g(x) = h(x)

这表明h(x)是一个偶函数。这一性质不仅反映了数学内在的和谐与统一，也为解决实际问题提供了新的视角和方法。

奇函数乘以奇函数等于偶函数这一规律，在多个领域都有着广泛的应用。比如在信号处理、量子力学以及工程学等领域，理解这种函数性质对于解析复杂系统的行为至关重要。此外，它也是学习更高级数学概念如傅里叶变换等的基础之一。

总之，奇函数乘以奇函数的结果是偶函数这一事实，虽然看似简单，却蕴含了丰富的数学内涵和广泛的应用前景。通过深入探索这些基本而又重要的数学规律，我们不仅能增进对数学美的认识，也能更好地理解和解决现实世界中的各种问题。

• 上一篇：nu11含义解析

• 下一篇：网络热梗：426背后的含义，你真的知道吗？